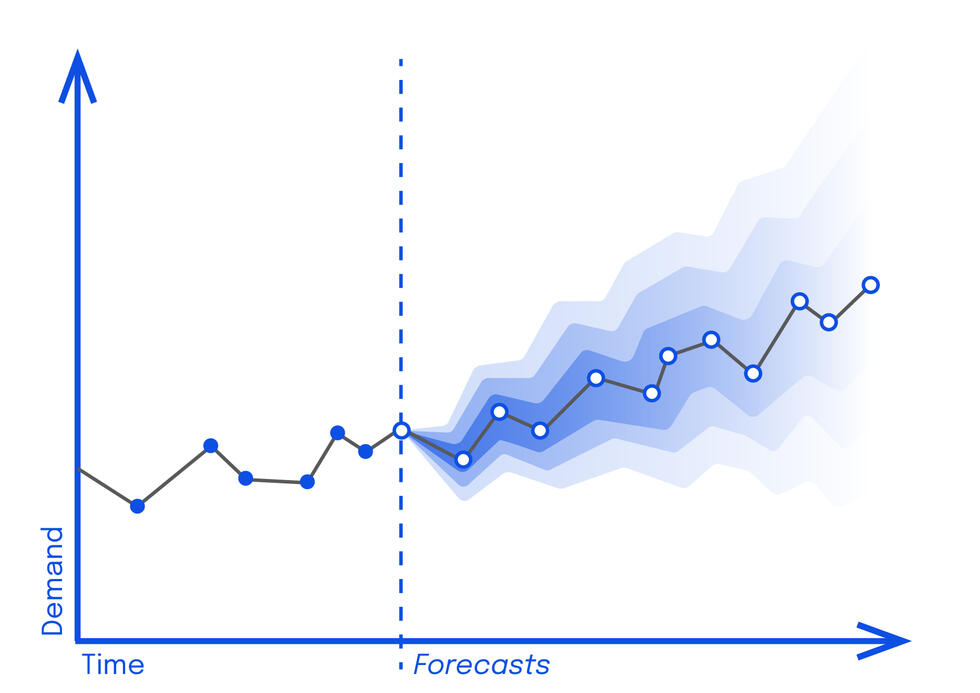
Zeitreihendaten bestehen aus Daten, die eine zeitliche Komponente beinhalten. Zum Beispiel die Anzahl der Verkäufe an einem bestimmten Tag, der schwankende Wert einer Aktie, die Durchschnittstemperatur in einer bestimmten Region usw.

Zeitreihendaten können kontinuierliche oder diskrete Werte haben und zeigen im Laufe der Zeit ein breites Spektrum an Verhaltensweisen:

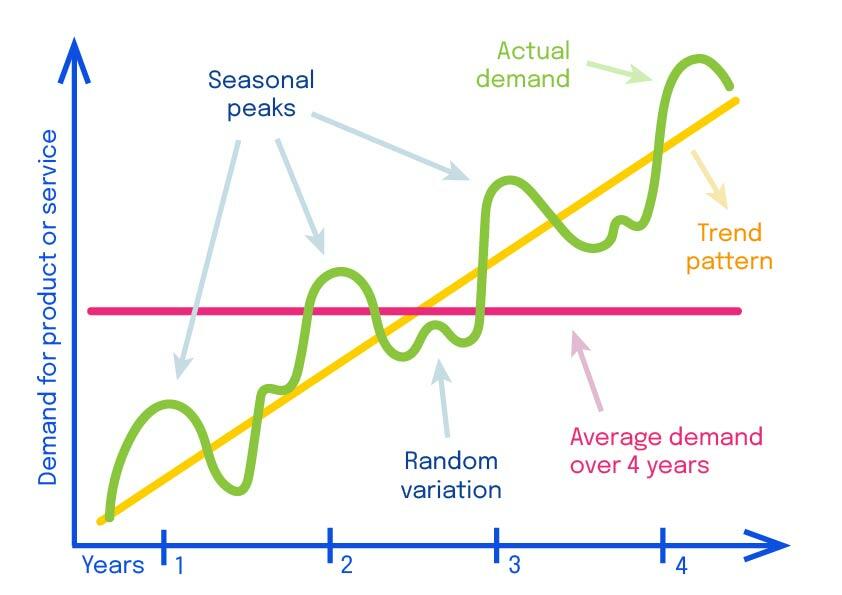
• Trends sind langfristige Muster, die in die gleiche allgemeine Richtung verlaufen.
• Zyklen sind nicht-periodische, wiederkehrende Muster, wie die Höhen und Tiefen des Aktienmarktes, bei denen die Zeitintervalle zwischen den Höhen und Tiefen variabel sind.
• Saisonalität hingegen ist ein Muster, das sich periodisch wiederholt (denken Sie beispielsweise an die höhere Nachfrage nach Geschenkpapier rund um Weihnachten).
• Schließlich sind Reaktionen auf äußere Einflüsse und zufällige Ereignisse mögliche Faktoren, die die zeitliche Entwicklung einer bestimmten Größe beeinflussen. Rauschen und Sparsamkeit erschweren es, ein Signal zu extrahieren und Vorhersagen zu treffen.

Zeitreihen sind oft miteinander abhängig und müssen daher gemeinsam betrachtet werden. Ein typisches Szenario ist, wenn eine Zeitreihe (eine Kovariate) verwendet wird, um Vorhersagen über eine andere (die Antwort oder Beobachtung) zu treffen. Zum Beispiel kann eine Zeitreihe, die angibt, ob ein Tag ein Feiertag ist oder nicht, als Kovariate (auch Merkmal genannt) verwendet werden, um tägliche Verkaufszahlen vorherzusagen.

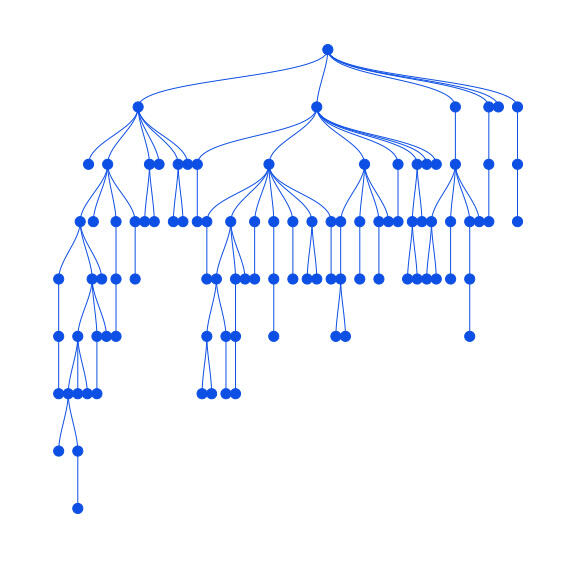
Darüber hinaus existieren in den meisten realen Fällen mehrere Zeitreihen in einer hierarchischen Struktur (hierarchische Zeitreihen). Zum Beispiel können die Verkaufszahlen verschiedener Produkte in Produktkategorien aggregiert werden, oder regionale Verkaufszahlen können in nationale Verkaufszahlen aggregiert werden.

Die Anzahl der einzelnen Zeitreihen in der gesamten Struktur kann sehr groß sein. Da sie auf der feinsten Ebene typischerweise spärlich und verrauscht sind, ermöglicht ihre Aggregation regelmäßigere Ergebnisse und eine leichtere Analyse.

(Automatische) Prognosen sind schwierig

Zeitreihen sind sehr nützlich, um die historische Entwicklung eines bestimmten Bereichs zu verstehen. Einige der häufigsten Fragen sind: Wie wird sich mein Produkt oder meine Dienstleistung in der Zukunft entwickeln? Wird der Trend anhalten? Sind die saisonalen Muster zuverlässig? Und wie sicher sind wir über diese Dinge?

Es wäre schön, immer einen Statistiker oder einen Zeitreihen-Experten zur Hand zu haben, um solche Fragen zu beantworten... aber Sie können sich wahrscheinlich vorstellen, dass dies nicht sehr praktisch und ziemlich teuer sein kann.

Automatische Prognosesysteme existieren daher, um auch in den Händen von Nicht-Experten vernünftige Vorhersagen zu ermöglichen.

Um automatisierte Antworten auf die oben genannten Fragen zu geben, müssen wir sicherstellen, dass das System wahrscheinlichkeitsbasierte Prognosen erstellt. Das bedeutet, dass die Prognose nicht nur aus einem einzelnen Wert besteht, der abweichen könnte (wie es historisch der Fall war), sondern aus einer Verteilung von Werten, die eine Schätzung der Unsicherheit berücksichtigt (was die Wahrscheinlichkeit darstellt, dass der tatsächliche Wert innerhalb eines Wertebereichs liegt). Wenn dies angemessen visualisiert wird, ermöglicht es auch Nicht-Experten, die Prognose zu bewerten.

Ein gutes Diagramm kann jedem schnell einen Überblick über die Bandbreite möglicher Ergebnisse und deren jeweilige Wahrscheinlichkeiten verschaffen.

Trotz der scheinbaren Einfachheit eines automatisch generierten Diagramms ist es sehr schwierig, automatische probabilistische Prognosen robust über viele Anwendungsfälle hinweg zu machen. Die Komplexität und Vielfalt der Zeitreihen (zeitliche Muster, Vielfalt der Datentypen, Rauschen, hierarchische Strukturen unterschiedlicher Art, Länge und Menge der Zeitreihen) stellen eine große Herausforderung dar.

Ohne die Anpassungen für Unsicherheit wissen wir nicht wirklich, wie zuverlässig die Prognose ist.

Zusätzlich sollten Prognosen für hierarchische Zeitreihen so entwickelt werden, dass sie kohärent sind. Zum Beispiel sollten Prognosen für aggregierte Verkaufszahlen mit der Aggregation der Prognosen für einzelne Verkaufszahlen übereinstimmen.

Prognosen für hierarchische Zeitreihen erfolgen normalerweise in zwei Schritten:

1. Zuerst werden Prognosen für jede einzelne Zeitreihe erstellt.

2. Im zweiten Schritt, der Konsolidierung genannt wird, werden diese Prognosen mit geeigneten probabilistischen Methoden angepasst, um kohärent zu werden. Dabei werden auch die Unsicherheitsschätzungen der einzelnen Serien auf sinnvolle Weise für die konsolidierten Prognosen kombiniert.

Hier ist ein visuelles Beispiel, wie die Konsolidierung funktioniert:

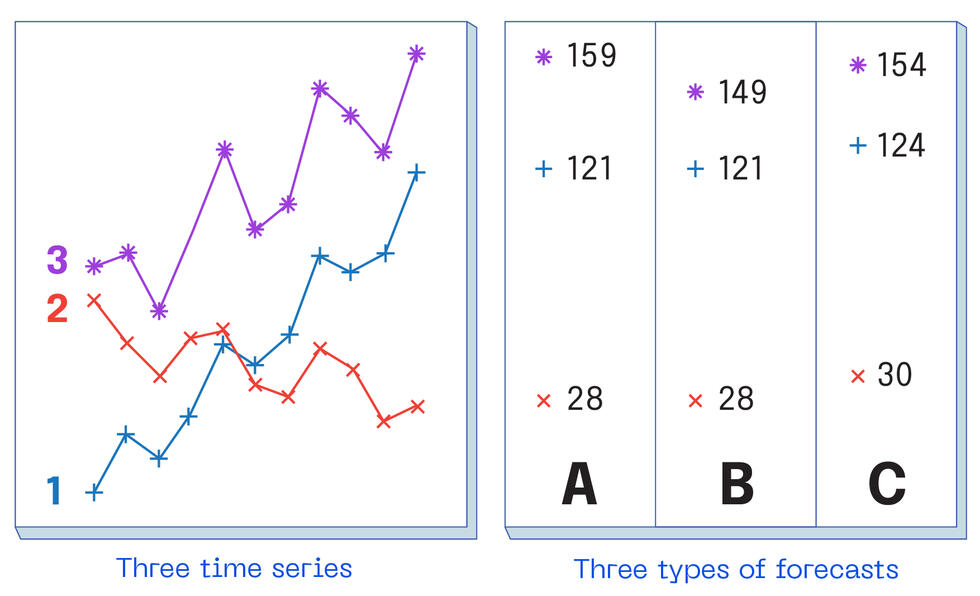
In der linken Abbildung sehen Sie die Entwicklung von drei Zeitreihen: 1 (blau) und 2 (rot), die historische Daten repräsentieren, sowie 3 (lila), die deren Summe ist.

In der rechten Abbildung finden wir drei Arten von Prognosen:

A zeigt die sogenannten „Basisprognosen“, bei denen jede Zeitreihe einzeln betrachtet wird, ohne zu berücksichtigen, dass 3 eine Summe der anderen ist.

B zeigt „Bottom-up-Prognosen“, die sich von den „Basisprognosen“ unterscheiden, da hier berücksichtigt wird, dass 3 die Summe der Zeitreihen 1 und 2 ist (d.h. 28 + 121 = 149). Diese Art der Prognose ist technisch kohärent, ist aber problematisch, da sie den Prognosen für 1 und 2 zu Unrecht Sicherheit verleiht. Zudem wird die lila Zeitreihe (Zeitreihe 3) nicht berücksichtigt.

C ist die Art von Prognose, die wir anstreben, bei der die drei Prognosen ein kohärentes Ergebnis liefern, in dem alle drei Basisprognosen gemäß ihrer Unsicherheit angepasst werden. Die Berücksichtigung der Unsicherheit ermöglicht eine Prognose, die wahrscheinlicher mit dem tatsächlichen Ergebnis übereinstimmt (allgemein mit dem Ziel von 90–95% Genauigkeit in der Vorhersage).

Wie bei den Modellen für einzelne Zeitreihen sollte die Konsolidierungsmethode robust gegenüber einer breiten Palette von Zeitreihenarten sein und idealerweise viele Arten von Abhängigkeiten berücksichtigen.

Zusammenfassend lässt sich sagen, dass die Entwicklung einer automatisierten Prognoselösung, die all diese verschiedenen Herausforderungen berücksichtigt, **nicht** einfach ist.

Sobald dieses Problem jedoch überwunden ist, können die daraus resultierenden maßgeschneiderten automatischen Prognosen in einen Workflow integriert werden, der von Entscheidungsträgern genutzt werden kann.

Kombination von Gaußschen Prozessen und probabilistischer Konsolidierung für automatische Prognosen

In dieser Phase könnten Sie sich fragen: Wie überwinden wir dieses Problem?

Gaußsche Prozesse (GPs) sind sehr flexible Modelle, die die Verteilung zwischen Variablen in Zeit und Raum definieren. In Kombination mit einer probabilistischen Konsolidierungsmethode lösen sie nahezu „out of the box“ all die oben genannten Herausforderungen.

GPs sind von Natur aus probabilistisch, da sie eine vollständige Verteilung über mögliche Entwicklungen einer Zeitreihe modellieren. Diese sogenannte Gaußsche Verteilung zeigt die Korrelation von Beobachtungen zu verschiedenen Zeitpunkten: Dies ermöglicht es uns, eine breite Palette von zeitlichen Verhaltensweisen zu erfassen. Die von GPs beschriebenen zeitlichen Muster bieten Vorlagen, die auf eine bestimmte Zeitreihe abgestimmt werden können, um Prognosen zu erstellen.

Die verschiedenen prognostizierten Bereiche können dann mit jedem neuen Datenpunkt auf kleinere Bereiche eingegrenzt werden. Stellen Sie sich vor, der GP hat bereits eine Vorstellung von den verschiedenen Trajektorien, die eine Zeitreihe nehmen könnte, aber jeder zusätzliche Datenpunkt schränkt diese auf Trajektorien ein, die wahrscheinlich tatsächlich eingetreten sind.

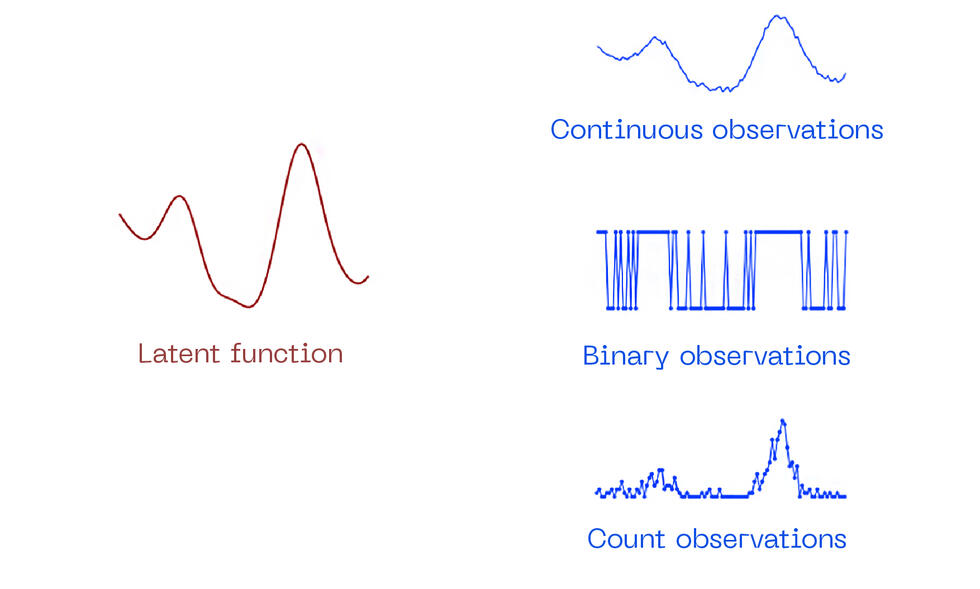
Zusätzlich können wir im zweiten Schritt verschiedene Verteilungen der gesammelten Daten erzeugen, indem wir den GP verwenden, um eine latente Funktion zu modellieren, die nicht direkt beobachtet wird, sondern über einen anderen zufälligen Prozess.

Dieses Zwei-Stufen-Modell mit nicht-Gaußschen Beobachtungen kann verwendet werden, um ein breiteres Spektrum an Daten zu beschreiben, das zuvor nicht erkannt wurde, und bessere Prognosen zu erstellen.

Natürlich ist diese Flexibilität und Leistung nicht einfach zu erreichen. Um GPs in der Praxis anzuwenden, müssen eine Reihe technischer Schwierigkeiten überwunden werden:

• Zunächst einmal kann ein einzelnes GP-Modell nicht auf alle Zeitreihen angewendet werden, da jede Zeitreihe unterschiedlich ist. Daher müssen für jede Zeitreihe individuell geeignete Parameterkonfigurationen gefunden werden.
• Nicht-Gaußsche Beobachtungen machen das Modell ebenfalls viel schwieriger zu handhaben, da Annäherungen verwendet werden müssen, um es besser verwaltbar zu machen.

In ihrer grundlegendsten Form skalieren GPs schlecht mit größeren Datensätzen aufgrund ihrer kubischen Komplexität in Bezug auf die Anzahl der Beobachtungen, was die Verarbeitungszeit des Algorithmus erheblich erhöht.

Diese Probleme haben die weitverbreitete Nutzung von GPs als Zeitreihenmodelle, insbesondere im Bereich der automatischen Prognosen, behindert.

Glücklicherweise haben jüngste Fortschritte dies verändert.

Moderne Approximationsmethoden, automatische Differenzierung und der Einsatz von GPU-Hardware ermöglichen es, GPs effizient auf größeren Datensätzen und mit nicht-Gaußschen Beobachtungen zu trainieren.

Dank dieser neuesten Innovationen sind automatische Prognosesysteme präziser und zuverlässiger als je zuvor. Das bedeutet, dass Sie mit besseren Vorhersagen Antworten auf Ihre „Was wäre wenn“-Fragen finden und fundiertere Entscheidungen für den Erfolg Ihres Unternehmens treffen können.